Electron. J. Diff. Eqns., Vol. 2001(2001), No. 12, pp. 1-9.
Asymptotic behavior of the solutions of a class of second order
differential systems
Svetoslav Ivanov Nenov
Abstract:
In the present paper it is proved that for any solution
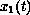 of the
system
of the
system
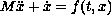 , for which
, for which
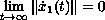 ,
there exists a solution
,
there exists a solution
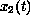 of the system
of the system
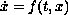 such that
such that
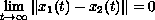 .
Some generalizations of this result are also presented.
The case
.
Some generalizations of this result are also presented.
The case
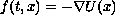 has been investigated explicitly.
has been investigated explicitly.
Submitted April 4, 2000; December 28, 2000. Published January 30, 2001.
Math Subject Classifications: 34D05, 34D10, 34E05.
Key Words: asymptotic behaviour, gradient systems, T. Wazewski's theorem.
Show me the
PDF file (150K),
TEX file, and other files for this article.
 |
Svetoslav Ivanov Nenov
Department of Mathematics
University of Chemical Technology and Metallurgy
8, Kliment Ohridsky blvd., Sofia 1756, Bulgaria
e-mail: s.nenov@uctm.edu, s_nenov@hotmail.com |
|---|
Return to the EJDE web page
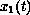 of the
system
of the
system
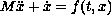 , for which
, for which
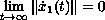 ,
there exists a solution
,
there exists a solution
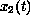 of the system
of the system
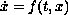 such that
such that
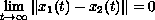 .
Some generalizations of this result are also presented.
The case
.
Some generalizations of this result are also presented.
The case
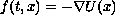 has been investigated explicitly.
has been investigated explicitly.
