Electron. J. Diff. Eqns., Vol. 2001(2001), No. 06, pp. 1-15.
Four-parameter bifurcation for a p-Laplacian system
Jacqueline Fleckinger, Rosa Pardo, & Francois de Thelin
Abstract:
We study a four-parameter bifurcation phenomenum arising in a
system involving
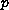 -Laplacians:
-Laplacians:
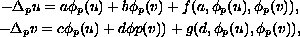
with
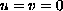 on the boundary of a bounded and sufficiently smooth domain in
on the boundary of a bounded and sufficiently smooth domain in
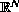 ;
here
;
here
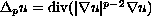 ,
with
,
with
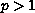 and
and
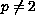 ,
is the
,
is the
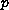 -Laplacian operator, and
-Laplacian operator, and
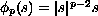 with
with
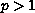 .
We assume that
.
We assume that
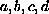 are real parameters. Then we
use a bifurcation method to exhibit some nontrivial solutions.
The associated eigenvalue problem, with
are real parameters. Then we
use a bifurcation method to exhibit some nontrivial solutions.
The associated eigenvalue problem, with
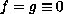 ,
is also studied here.
,
is also studied here.
Submitted June 29, 2000. Published January 9, 2001.
Math Subject Classifications: 35J45, 35J55, 35J60, 35J65, 35J30, 35P30.
Key Words: p-Laplacian, bifurcation.
Show me the
PDF file (181K),
TEX file, and other files for this article.
 |
Jacqueline Fleckinger
CEREMATH & UMR MIP, Universite Toulouse 1
pl. A. France
31042 Toulouse Cedex, France
e-mail: jfleck@univ-tlse1.fr |
|---|
 |
Rosa Pardo
Departamento de Matematica Aplicada
Universidad Complutense de Madrid
Madrid 28040, Spain
e-mail: rpardo@sunma4.mat.ucm.es |
|---|
 |
Francois de Thelin
UMR MIP, Universite Toulouse 3
118 route de Narbonne
31062 Toulouse Cedex 04, France
e-mail: dethelin@mip.ups-tlse.fr |
|---|
Return to the EJDE web page
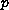 -Laplacians:
-Laplacians:
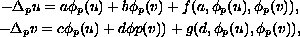
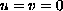 on the boundary of a bounded and sufficiently smooth domain in
on the boundary of a bounded and sufficiently smooth domain in
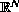 ;
here
;
here
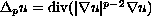 ,
with
,
with
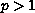 and
and
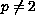 ,
is the
,
is the
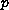 -Laplacian operator, and
-Laplacian operator, and
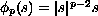 with
with
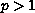 .
We assume that
.
We assume that
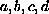 are real parameters. Then we
use a bifurcation method to exhibit some nontrivial solutions.
The associated eigenvalue problem, with
are real parameters. Then we
use a bifurcation method to exhibit some nontrivial solutions.
The associated eigenvalue problem, with
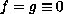 ,
is also studied here.
,
is also studied here. 

