Electron. J. Diff. Eqns., Vol. 2001(2001), No. 01, pp. 1-26.
On the singularities of 3-D Protter's problem for the wave equation
Myron K. Grammatikopoulos, Tzvetan D. Hristov, & Nedyu I. Popivanov
Abstract:
In this paper we study boundary-value problems for the wave equation, which
are three-dimensional analogue of Darboux-problems (or of Cauchy-Goursat
problems) on the plane. It is shown that for
 in
in
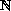 there
exists a right hand side smooth function from
there
exists a right hand side smooth function from
 , for
which the corresponding unique generalized solution belongs to
, for
which the corresponding unique generalized solution belongs to
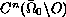 , and it has a strong power-type
singularity at the point
, and it has a strong power-type
singularity at the point
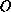 .
This singularity is isolated at the vertex
.
This singularity is isolated at the vertex
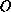 of the characteristic cone and does not propagate along the cone.
In this paper we investigate the behavior of the singular solutions at the point
of the characteristic cone and does not propagate along the cone.
In this paper we investigate the behavior of the singular solutions at the point
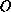 . Also,
we study more general boundary-value problems and find that there exist an
infinite number of smooth right-hand side functions for which the
corresponding unique generalized solutions are singular. Some a priori
estimates are also stated.
. Also,
we study more general boundary-value problems and find that there exist an
infinite number of smooth right-hand side functions for which the
corresponding unique generalized solutions are singular. Some a priori
estimates are also stated.
Submitted October 30, 2000. Published January 1, 2001.
Math Subject Classifications: 35L05, 35L20, 35D05, 35A20.
Key Words: Wave equation, boundary-value problems, generalized solution,
singular solutions, propagation of singularities.
Show me the
PDF file (243K),
TEX file, and other files for this article.
 |
Myron K. Grammatikopoulos
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: mgrammat@cc.uoi.gr |
|---|
 |
Tzvetan D. Hristov
Institute of Mathematics and Informatics
Bulgarian Academy of Sciences
1113 Sofia, Bulgaria
email: tzvetan@math.bas.bg |
|---|
 |
Nedyu I. Popivanov
Department of Mathematics and Informatics
University of Sofia
1164 Sofia, Bulgaria
email: nedyu@fmi.uni-sofia.bg |
|---|
Return to the EJDE web page
 in
in
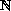 there
exists a right hand side smooth function from
there
exists a right hand side smooth function from
 , for
which the corresponding unique generalized solution belongs to
, for
which the corresponding unique generalized solution belongs to
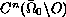 , and it has a strong power-type
singularity at the point
, and it has a strong power-type
singularity at the point
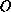 .
This singularity is isolated at the vertex
.
This singularity is isolated at the vertex
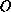 of the characteristic cone and does not propagate along the cone.
In this paper we investigate the behavior of the singular solutions at the point
of the characteristic cone and does not propagate along the cone.
In this paper we investigate the behavior of the singular solutions at the point
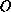 . Also,
we study more general boundary-value problems and find that there exist an
infinite number of smooth right-hand side functions for which the
corresponding unique generalized solutions are singular. Some a priori
estimates are also stated.
. Also,
we study more general boundary-value problems and find that there exist an
infinite number of smooth right-hand side functions for which the
corresponding unique generalized solutions are singular. Some a priori
estimates are also stated. 

