Electron. J. Diff. Eqns., Vol. 2000(2000), No. 59, pp. 1-8.
Differential operators on equivariant vector bundles over symmetric spaces
Anton Deitmar
Abstract:
Generalizing the algebra of motion-invariant differential
operators on a symmetric space we study invariant operators on
equivariant vector bundles. We show that the eigenequation is
equivalent to the corresponding eigenequation with respect to
the larger algebra of all invariant operators. We compute the
possible eigencharacters and show that for invariant integral
operators the eigencharacter is given by the Abel transform.
We show that sufficiently regular operators are surjective,
i.e. that equations of the form
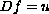 are solvable for all
are solvable for all
 .
.
An addendum to this article was attached on February 26, 2001.
In this addendum, the original proof of Theorem 4.4 is expanded.
Submitted May 16, 2000. Published September 1, 2000.
Math Subject Classifications: 43A85, 22E30, 35J45.
Key Words: invariant operators.
Show me the
PDF file (256K),
TEX file, and other files for this article.
 |
Anton Deitmar
School of Mathematical Sciences
University of Exeter
Laver Building, North Park Road
Exeter, EX4 4QE
Devon, UK
email: A.H.J.Deitmar@exeter.ac.uk
|
Return to the EJDE web page
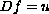 are solvable for all
are solvable for all
 .
.
