Electron. J. Diff. Eqns., Vol. 2000(2000), No. 44, pp. 1-11.
Symmetry theorems via the continuous steiner symmetrization
L. Ragoub
Abstract:
Using a new approach due to F. Brock called the Steiner symmetrization,
we show first that if

is a solution of an
overdetermined problem in the divergence form satisfying the Neumann
and non-constant Dirichlet boundary conditions, then
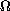 is an N-ball.
In addition, we show that we can relax the condition on
the value of the Dirichlet boundary condition in the case of
superharmonicity.
Finally, we give an application to positive solutions of some
semilinear elliptic problems in symmetric domains for the divergence case.
is an N-ball.
In addition, we show that we can relax the condition on
the value of the Dirichlet boundary condition in the case of
superharmonicity.
Finally, we give an application to positive solutions of some
semilinear elliptic problems in symmetric domains for the divergence case.
Submitted October 1, 1999. Published June 12, 2000.
Math Subject Classifications: 28D10, 35B05, 35B50, 35J25, 35J60, 35J65.
Key Words: Moving plane method, Steiner Symmetrization,
Overdetermined problems, Local Symmetry.
Show me the
PDF file (137K),
TEX file, and other files for this article.
L. Ragoub
Riyadh College of Technology, Mathematics Department
P.O.Box 42, 826 Riyadh 11 551, Saudi Arabia
e-mail: f66m002@ksu.edu.sa
Return to the EJDE web page

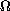 is an N-ball.
In addition, we show that we can relax the condition on
the value of the Dirichlet boundary condition in the case of
superharmonicity.
Finally, we give an application to positive solutions of some
semilinear elliptic problems in symmetric domains for the divergence case.
is an N-ball.
In addition, we show that we can relax the condition on
the value of the Dirichlet boundary condition in the case of
superharmonicity.
Finally, we give an application to positive solutions of some
semilinear elliptic problems in symmetric domains for the divergence case.