Electron. J. Diff. Eqns., Vol. 2000(2000), No. 43, pp. 1-8.
Uniqueness of solutions to a system of differential inclusions
Chunpeng Wang & Jingxue Yin
Abstract:
In this paper we study the uniqueness of solutions to
the initial and Dirichlet boundary-value problem of
differential inclusions
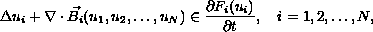
where
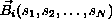 is an
n-dimensional vector continuously differentiable on
is an
n-dimensional vector continuously differentiable on
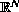 ,
and
,
and
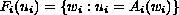 ,
,
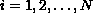 with
with
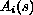 continuously differentiable functions on
continuously differentiable functions on
 and
and
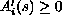 .
.
Submitted May 15, 2000. Published June 12, 2000.
Math Subject Classifications: 35K50, 35K65, 35A05, 35D99.
Key Words: differential inclusions, degeneracy, uniqueness.
Show me the
PDF file (129K),
TEX file, and other files for this article.
 |
Chunpeng Wang
Department of Mathematics
JiLin University
Changchun, Jilin 130023, People's Republic of China |
 |
Jingxue Yin
Department of Mathematics
JiLin University
Changchun, Jilin 130023, People's Republic of China
e-mail: yjx@mail.jlu.edu.cn |
Return to the EJDE web page
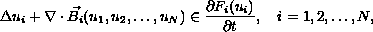
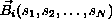 is an
n-dimensional vector continuously differentiable on
is an
n-dimensional vector continuously differentiable on
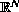 ,
and
,
and
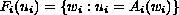 ,
,
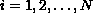 with
with
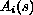 continuously differentiable functions on
continuously differentiable functions on
 and
and
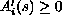 .
.

