Electron. J. Diff. Eqns., Vol. 2000(2000), No. 39, pp. 1-17.
Regular oblique derivative problem in Morrey spaces
Dian K. Palagachev, Maria Alessandra Ragusa, & Lubomira G. Softova
Abstract:
This article presents a study of the regular oblique derivative problem

Assuming that the coefficients
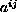 belong to the Sarason's class
of functions with vanishing mean oscillation, we show existence and
global regularity of strong solutions in Morrey spaces.
belong to the Sarason's class
of functions with vanishing mean oscillation, we show existence and
global regularity of strong solutions in Morrey spaces.
Submitted December 17, 1999. Published May 23, 2000.
Math Subject Classifications: 35J25, 35B65, 35R05
Key Words: Uniformly elliptic operator, regular oblique derivative problem,
Morrey spaces.
Show me the
PDF file (214K),
TEX file, and other files for this article.
 |
Dian K. Palagachev
Dipartimento Interuniversitario di Matematica
Politecnico di Bari,
Via E. Orabona, 4, 70125 Bari, Italy
email: dian@pascal.dm.uniba.it |
 |
Maria Alessandra Ragusa
Dipartimento di Matematica, Universita di Catania,
Viale A. Doria, 6, 95125 Catania, Italy
email: maragusa@dipmat.unict.it |
 |
Lubomira G. Softova
Bulgarian Academy of Sciences
Institute of Mathematics and Informatics,
Dept. Math. Physics,
``Acad. G. Bonchev'' Str., bl. 8, 1113 Sofia, Bulgaria
email: luba@dipmat.unict.it |
Return to the EJDE web page

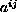 belong to the Sarason's class
of functions with vanishing mean oscillation, we show existence and
global regularity of strong solutions in Morrey spaces.
belong to the Sarason's class
of functions with vanishing mean oscillation, we show existence and
global regularity of strong solutions in Morrey spaces. 

