Electron. J. Diff. Eqns., Vol. 2000(2000), No. 37, pp. 1-21.
Resonance with respect to the Fucik spectrum
A. K. Ben-Naoum, C. Fabry, & D. Smets
Abstract:
Let
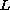 be a self-adjoint operator on
be a self-adjoint operator on
 with
with
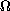 a bounded and open subset of
a bounded and open subset of
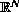 .
This article considers the resonance problem
with respect to the Fucik spectrum of
.
This article considers the resonance problem
with respect to the Fucik spectrum of
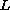 ,
which means that we study equations of the form
,
which means that we study equations of the form
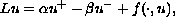
when the homogeneous equation
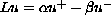 has non-trivial solutions. Using the computation of degrees that are
not necessarily +1 or -1, we present results about the
existence of solutions. Our results are illustrated
with examples and can be seen as generalizations of Landesman-Lazer
conditions. Non-existence results are also given.
has non-trivial solutions. Using the computation of degrees that are
not necessarily +1 or -1, we present results about the
existence of solutions. Our results are illustrated
with examples and can be seen as generalizations of Landesman-Lazer
conditions. Non-existence results are also given.
Submitted January 4, 2000. Published May 17, 2000.
Math Subject Classifications: 70K30, 35P30, 35G30.
Key Words: Resonance, jumping nonlinearity, Landesman-Lazer conditions.
Show me the
PDF file (210K),
TEX file, and other files for this article.
 |
A. K. Ben-Naoum
Universite de Mons - Hainaut
Institut de mathematique et d'informatique
6 Avenue du Champ de Mars, B - 7000 Mons, Belgium
e-mail: kbn@bsb.be |
 |
C. Fabry
Universite catholique de Louvain
Departement de mathematique
2 Chemin du cyclotron, B - 1348 Louvain-la-Neuve, Belgium
e-mail: fabry@math.ucl.ac.be |
 |
Didier Smets
Universite catholique de Louvain
Departement de mathematique
2 Chemin du cyclotron, B - 1348 Louvain-la-Neuve, Belgium
e-mail: smets@amm.ucl.ac.be |
Return to the EJDE web page
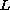 be a self-adjoint operator on
be a self-adjoint operator on
 with
with
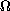 a bounded and open subset of
a bounded and open subset of
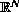 .
This article considers the resonance problem
with respect to the Fucik spectrum of
.
This article considers the resonance problem
with respect to the Fucik spectrum of
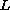 ,
which means that we study equations of the form
,
which means that we study equations of the form
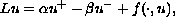
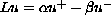 has non-trivial solutions. Using the computation of degrees that are
not necessarily +1 or -1, we present results about the
existence of solutions. Our results are illustrated
with examples and can be seen as generalizations of Landesman-Lazer
conditions. Non-existence results are also given.
has non-trivial solutions. Using the computation of degrees that are
not necessarily +1 or -1, we present results about the
existence of solutions. Our results are illustrated
with examples and can be seen as generalizations of Landesman-Lazer
conditions. Non-existence results are also given.

