Electron. J. Diff. Eqns., Vol. 2000(2000), No. 36, pp. 1-10.
Global minimizing domains for the first eigenvalue of an elliptic
operator with non-constant coefficients
Dorin Bucur & Nicolas Varchon
Abstract:
We consider an elliptic operator, in divergence form, that is a
uniformly elliptic matrix. We describe the behavior of every sequence
of domains which minimizes the first Dirichlet eigenvalue over a
family of fixed measure domains of
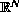 .
The existence of minimizers is proved in some particular situations,
for example when the operator is periodic.
.
The existence of minimizers is proved in some particular situations,
for example when the operator is periodic.
Submitted February 1-st, 2000. Published May 16, 2000.
Math Subject Classifications: 49Q10, 49R50.
Key Words: First eigenvalue, Dirichlet boundary, non-constant coeffcients,
optimal domain.
Show me the
PDF file (155K),
TEX file, and other files for this article.
 |
Dorin Bucur
Equipe de Mathematiques, UMR CNRS 6623
Universite; de Franche-Comte
16, route de Gray, 25030 Besancon Cedex, France
email: bucur@math.univ-fcomte.fr |
 |
Nicolas Varchon
Equipe de Mathematiques, UMR CNRS 6623
Universite; de Franche-Comte
16, route de Gray, 25030 Besancon Cedex, France
email: varchon@math.univ-fcomte.fr |
Return to the EJDE web page
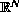 .
The existence of minimizers is proved in some particular situations,
for example when the operator is periodic.
.
The existence of minimizers is proved in some particular situations,
for example when the operator is periodic. 
