Electron. J. Diff. Eqns., Vol. 2000(2000), No. 30, pp. 1-22.
Viscous profiles for traveling waves of scalar balance laws:
The uniformly hyperbolic case
Joerg Haerterich
Abstract:
We consider a scalar hyperbolic conservation law with a nonlinear source term
and viscosity
 .
For
.
For  =0, there exist in general
different types of heteroclinic entropy traveling waves. It is shown
that for
=0, there exist in general
different types of heteroclinic entropy traveling waves. It is shown
that for
 positive and sufficiently small the viscous equation possesses
similar traveling wave solutions and that the profiles converge in
exponentially weighted
positive and sufficiently small the viscous equation possesses
similar traveling wave solutions and that the profiles converge in
exponentially weighted
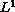 -norms as
-norms as
 decreases
to zero.
The proof is based on a careful study of the singularly perturbed second-order
equation that arises from the traveling wave ansatz.
decreases
to zero.
The proof is based on a careful study of the singularly perturbed second-order
equation that arises from the traveling wave ansatz.
Submitted February 22, 2000. Published April 25, 2000.
Math Subject Classifications: 35B25, 35L65, 34C37.
Key Words: Hyperbolic conservation laws, source terms, traveling waves,
viscous profiles, singular perturbations.
Show me the
PDF file (206K),
TEX file, and other files for this article.
 |
Jörg Härterich
Freie Universitat Berlin,
Arnimallee 2-6,
D-14195 Berlin, Germany
e-mail: haerter@math.fu-berlin.de
|
Return to the EJDE web page
 .
For
.
For  =0, there exist in general
different types of heteroclinic entropy traveling waves. It is shown
that for
=0, there exist in general
different types of heteroclinic entropy traveling waves. It is shown
that for
 positive and sufficiently small the viscous equation possesses
similar traveling wave solutions and that the profiles converge in
exponentially weighted
positive and sufficiently small the viscous equation possesses
similar traveling wave solutions and that the profiles converge in
exponentially weighted
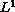 -norms as
-norms as
 decreases
to zero.
The proof is based on a careful study of the singularly perturbed second-order
equation that arises from the traveling wave ansatz.
decreases
to zero.
The proof is based on a careful study of the singularly perturbed second-order
equation that arises from the traveling wave ansatz. 