We consider three nonlinear eigenvalue problems that consist of
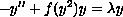
with one of the following boundary conditions:
y(0)=y(1)=0 y'(0)=p,
y'(0)=y(1)=0 y(0)=p,
y'(0)=y'(1)=0 y(0)=p,
where p is a positive constant. Under smoothness and monotonicity conditions on f, we show the existence and uniqueness of a sequence of eigenvalues
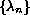 and corresponding eigenfunctions
and corresponding eigenfunctions
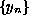 such that
such that
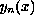 has precisely n roots in the interval (0,1),
where n=0,1,2,....
has precisely n roots in the interval (0,1),
where n=0,1,2,.... For the first boundary condition, we show that
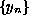 is a basis and that
is a basis and that
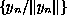 is a Riesz basis in the space
is a Riesz basis in the space
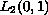 .
For the second and third boundary conditions, we show that
.
For the second and third boundary conditions, we show that
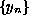 is a Riesz basis.
is a Riesz basis. 