Electron. J. Diff. Eqns., Vol. 2000(2000), No. 17, pp. 1-17.

Existence results for singular anisotropic elliptic boundary-value problems

Eun Heui Kim

Abstract:
We establish the existence of a positive solution for anisotropic singular quasilinear elliptic boundary-value problems. As an example of the problems studied we have
$$ u^au_{xx}+u^bu_{yy}+\lambda(u+1)^{a+r}=0 $$
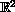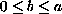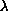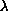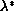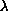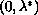with zero Dirichlet boundary condition, on a bounded convex domain in ${\Bbb R}^2$. Here $0\leq b\leq a$, and $\lambda$, r are positive constants. When 0< r< 1 (sublinear case), for each positive $\lambda$ there exists a positive solution. On the other hand when r>1 (superlinear case), there exists a positive constant $\lambda^*$ such that for $\lambda$ in $(0,\lambda^*)$ there exists a positive solution, and for 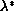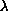$\lambda^*$ < $\lambda$ there is no positive solution.

Submitted January 11, 2000. Published February 29, 2000.
Math Subject Classifications: 35J65, 35J70.
Key Words: anisotropic, singular, sublinear, superlinear, elliptic boundary-value problems.

Show me the PDF file (193K), TEX file, and other files for this article.

Eun Heui Kim
Department of Mathematics, University of Houston
Houston, TX 77204-3476 USA
email: ehkim@math.uh.edu
Return to the EJDE web page