Electron.n. J. Diff. Eqns., Vol. 1999(1999), No. 09, pp. 1-29.
Boundary-value problems for the one-dimensional
p-Laplacian with even superlinearity
Idris Addou & Abdelhamid Benmezai
Abstract:
This paper is concerned with a study of the quasilinear problem
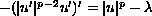 , in (0,1)
, in (0,1)
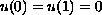 ,
,
where 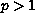 and
and
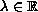 are parameters.
For
are parameters.
For 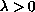 ,
we determine a lower bound for the number of solutions
and establish their nodal properties. For
,
we determine a lower bound for the number of solutions
and establish their nodal properties. For
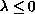 ,
we determine the exact number of solutions.
In both cases we use a quadrature method.
,
we determine the exact number of solutions.
In both cases we use a quadrature method.
Submitted October 28, 1998. Published March 8, 1999.
Math Subject Classification: 34B15, 34C10.
Key Words: One-dimensional p-Laplacian, two-point
boundary-value problem, superlinear, time mapping.
Show me the
PDF file (236K),
TEX file, and other files for this article.
 |
Idris Addou
USTHB, Institut de Mathematiques
El-Alia, B.P. no. 32 Bab-Ezzouar
16111, Alger, Algerie.
e-mail: idrisaddou@hotmail.com |
| |
Abdelhamid Benmezai
USTHB, Institut de Mathematiques
El-Alia, B.P. no. 32 Bab-Ezzouar
16111, Alger, Algerie. |
Return to the EJDE web page
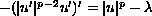 , in (0,1)
, in (0,1)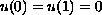 ,
, 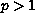 and
and
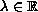 are parameters.
For
are parameters.
For 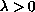 ,
we determine a lower bound for the number of solutions
and establish their nodal properties. For
,
we determine a lower bound for the number of solutions
and establish their nodal properties. For
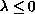 ,
we determine the exact number of solutions.
In both cases we use a quadrature method.
,
we determine the exact number of solutions.
In both cases we use a quadrature method. 