We study the regularity of a moving interface
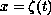 of the solutions for the initial value problem
of the solutions for the initial value problem 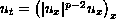
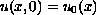 ,
,where
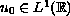 and
and
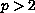 .
We prove that each side of the moving interface is
.
We prove that each side of the moving interface is
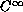 .
.
Yoonmi Ham & Youngsang Ko
Abstract:
We study the regularity of a moving interface
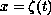 of the solutions for the initial value problem
of the solutions for the initial value problem
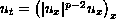
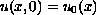 ,
,
where
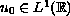 and
and
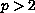 .
We prove that each side of the moving interface is
.
We prove that each side of the moving interface is
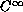 .
.
Submitted November 11, 1998. Published January 5, 1999.
Math Subject Classification: 35K65.
Key Words: p-Laplacian, free boundary, C-infinity regularity
Show me the PDF file (156K), TEX file, and other files for this article.
Youngsang Ko
Department of Mathematics,
Kyonggi University
Suwon, Kyonggi-do, 442-760, Korea
e-mail: ysgo@kuic.kyonggi.ac.kr