Electron. J. Diff. Eqns., Vol. 1998(1998), No. 35, pp. 1-7.
Eigenvalue Comparisons for Differential Equations on a Measure Chain
Chuan Jen Chyan, John M. Davis,
Johnny Henderson, & William K. C. Yin
Abstract:
The theory of u0-positive operators with respect to a
cone in a Banach space is applied to eigenvalue problems associated with the
second order
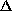 -differential
equation (often referred to as a differential equation on a measure chain)
given by
-differential
equation (often referred to as a differential equation on a measure chain)
given by
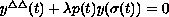 ,
,
![$t\in[0,1]$](gifs/ac.gif) ,
,
satisfying the boundary conditions
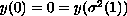 .
The existence of a smallest positive eigenvalue is proven and then a theorem
is established comparing the smallest positive eigenvalues for two problems
of this type.
.
The existence of a smallest positive eigenvalue is proven and then a theorem
is established comparing the smallest positive eigenvalues for two problems
of this type.
Submitted November 23, 1998. Published December 19, 1998.
Math Subject Classification: 34B99, 39A99.
Key Words: Measure chain, eigenvalue problem
Show me the
PDF file (132K),
TEX file, and other files for this article.
Chuan Jen Chyan
Department of Mathematics,
Tamkang University,
Taipei, Taiwan
e-mail: chuanjen@mail.tku.edu.tw
John M. Davis
Department of Mathematics,
Auburn University,
Auburn, AL 36849 USA
e-mail: davis05@mail.auburn.edu
Johnny Henderson
Department of Mathematics,
Auburn University,
Auburn, AL 36849 USA
e-mail: hendej2@mail.auburn.edu
William K. C. Yin
Department of Mathematics,
LaGrange College,
LaGrange, GA 30240 USA
e-mail: wyin@lgc.edu
Return to the EJDE web page
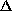 -differential
equation (often referred to as a differential equation on a measure chain)
given by
-differential
equation (often referred to as a differential equation on a measure chain)
given by 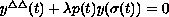 ,
,
![$t\in[0,1]$](gifs/ac.gif) ,
, 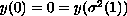 .
The existence of a smallest positive eigenvalue is proven and then a theorem
is established comparing the smallest positive eigenvalues for two problems
of this type.
.
The existence of a smallest positive eigenvalue is proven and then a theorem
is established comparing the smallest positive eigenvalues for two problems
of this type.