Electron. J. Diff. Eqns., Vol. 1998(1998), No. 20, pp. 1-20.

The Schrodinger equation on non-stationary domains

Gunther Karner

Abstract:
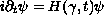We investigate the dynamical effects of non-stationary boundaries on the stability of a quantum Hamiltonian system described by a periodic family $\{H(\gamma,t), t\in[0,\Gamma],\Gamma positive\}$ of Sturm-Liouville operators, a Schrodinger equation $i\partial_{t}\psi = H(\gamma,t)\psi$ defined on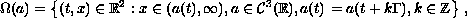
$$\Omega (a) = \left\{(t,x)\in{\Bbb R}^2 : x\in{(a(t),\infty)}, a\in{\cal C}^3({\Bbb R}),a(t)=a(t+k\Gamma), k\in{\Bbb Z}\right\}\,,$$
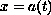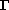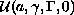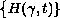as well as boundary conditions at $x=a(t)$ modeled by the $\Gamma$-periodic function $\gamma$. Employing extended Hilbert space methods, stability conditions for the spectra of the evolution operators ${\cal U}(a,\gamma,\Gamma,0)$ to the families $\bigl\{H(\gamma,t)\}$ under perturbations induced by variations of boundary oscillations, respectively conditions, are derived. 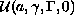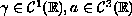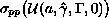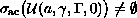In particular, it is shown that the existence of a pure point finitely degenerate realization ${\cal U}(a,\hat{\gamma},\Gamma,0))$ implies pure point ${\cal U}(a,\gamma,\Gamma,0)$ for all $\gamma\in{\cal C}^1({\Bbb R}), a\in{\cal C}^3({\Bbb R})$, whereas in case of infinitely degenerate $\sigma_{pp}\bigl({\cal U}(a,\hat{\gamma},\Gamma,0)\bigr)$ the existence of $\sigma_{{\rm ac}}\bigl({\cal U}(a,\gamma,\Gamma,0)\bigr)\neq\emptyset$, respectively $\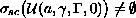sigma_{sc}\bigl({\cal U}(a,\gamma,\Gamma,0)\bigr)\neq\emptyset$, is possible.

Submitted December 18, 1997. Published July 17, 1998.
Math Subject Classification: 35P05, 81Q10.
Key Words: Stability of dense point spectra, boundary induced perturbations, Krein's resolvent formula.

Show me the PDF file (235 KB), TEX file, and other files for this article.

Gunther Karner
Institut fur Kerntechnik und Reaktorsicherheit
Universitat Karlsruhe (TH), Postfach 3640
D - 76021 Karlsruhe, Germany
e-mail: karner@irs.fzk.de
http://ikrshp2.mach.uni-karlsruhe.de/karner/homepage.html
Return to the EJDE home page