Electron. J. Diff. Eqns.,
Vol. 1998(1998), No. 08, pp. 1-21.
Existence and boundary stabilization of a nonlinear hyperbolic equation
with time-dependent coefficients
M. M. Cavalcanti, V. N. Domingos Cavalcanti & J. A. Soriano
Abstract:
In this article, we study the hyperbolic problem
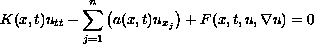
coupled with boundary conditions
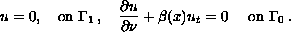
Here the variable
 belongs to a bounded region of
belongs to a bounded region of
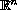 , whose
boundary is partitioned into two disjoint sets
, whose
boundary is partitioned into two disjoint sets
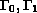 .
.
We prove existence, uniqueness, and uniform stability of strong and weak
solutions when the coefficients and the boundary conditions
provide a damping effect.
Submitted July 6, 1997. Published March 10, 1998.
Math Subject Classification: 35B40, 35L80.
Key Words: Boundary stabilization, asymptotic behaviour.
Show me the
PDF file (208 KB),
TEX file, and other files for this article.
 |
Marcelo M. Cavalcanti
Universidade Estadual de Maringa,
87020-900 Maringa-PR, Brazil
e-mail: marcelo@gauss.dma.uem.br
|
|---|
 |
Valeria N. Domingos Cavalcanti
Universidade Estadual de Maringa,
87020-900 Maringa-PR, Brazil
e-mail: valeria@gauss.dma.uem.br
|
|---|
 |
Juan Amadeo Soraino
Universidade Estadual de Maringa,
87020-900 Maringa-PR, Brazil
e-mail: soriano@gauss.dma.uem.br
|
|---|
Return to the EJDE home page
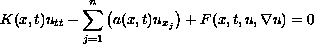
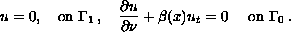
 belongs to a bounded region of
belongs to a bounded region of
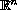 , whose
boundary is partitioned into two disjoint sets
, whose
boundary is partitioned into two disjoint sets
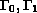 .
.


