Electron. J. Diff. Eqns.,
Vol. 1997(1997), No. 24, pp. 1-20.
Initial value problems for nonlinear nonresonant delay
differential equations with possibly infinite delay
Lance D. Drager & William Layton
Abstract:
We study initial value problems for scalar, nonlinear, delay
differential equations with distributed, possibly infinite, delays.
We consider the
initial value problem
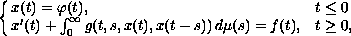
where
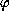 and
and
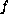 are bounded and
are bounded and
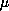 is a finite
Borel measure. Motivated by the nonresonance condition for the
linear case and previous work of the authors, we introduce conditions
on
is a finite
Borel measure. Motivated by the nonresonance condition for the
linear case and previous work of the authors, we introduce conditions
on
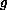 . Under these conditions, we prove an existence and uniqueness
theorem. We show that under the same
conditions, the solutions are globally
asymptotically stable and, if
. Under these conditions, we prove an existence and uniqueness
theorem. We show that under the same
conditions, the solutions are globally
asymptotically stable and, if
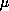 satisfies an exponential decay
condition, globally exponentially asymptotically stable.
satisfies an exponential decay
condition, globally exponentially asymptotically stable.
Submitted August 14, 1997. Published December 19, 1997.
Math Subject Classification: 34K05, 34K20, 34K25
Key Words: Delay differential equation, infinite delay, initial value problem,
nonresonance, asymptotic stability, exponential asymptotic stability.
Show me the
PDF file (204 KB),
TEX file, and other files for this article.
Lance D. Drager
Department of Mathematics and Statistics;
Texas Tech University;
Lubbock, TX 79409-1042 USA.
e-mail: drager@math.ttu.edu
William Layton
Department of Mathematics;
University of Pittsburgh;
Pittsburgh, PA 15260 USA.
e-mail: wjl+@pitt.edu
Return to the EJDE home page
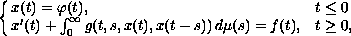
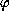 and
and
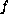 are bounded and
are bounded and
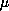 is a finite
Borel measure. Motivated by the nonresonance condition for the
linear case and previous work of the authors, we introduce conditions
on
is a finite
Borel measure. Motivated by the nonresonance condition for the
linear case and previous work of the authors, we introduce conditions
on
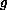 . Under these conditions, we prove an existence and uniqueness
theorem. We show that under the same
conditions, the solutions are globally
asymptotically stable and, if
. Under these conditions, we prove an existence and uniqueness
theorem. We show that under the same
conditions, the solutions are globally
asymptotically stable and, if
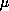 satisfies an exponential decay
condition, globally exponentially asymptotically stable.
satisfies an exponential decay
condition, globally exponentially asymptotically stable.