Electron. J. Diff. Eqns., Vol. 1997(1997), No. 13, pp 1-10.

Multiple positive solutions for equations involving critical Sobolev exponent in ${\Bbb R}^N$

C. O. Alves

Abstract:
This article concerns with the problem
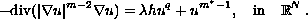
$$ -{\rm div }(|\nabla u|^{m-2}\nabla u) = \lambda h u^q+u^{m^*-1},\quad{\rm in}\quad {\Bbb R}^N\,. $$
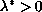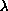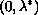Using the Ekeland Variational Principle and the Mountain Pass Theorem, we show the existence of $\lambda ^*>0$ such that there are at least two non-negative solutions for each $\lambda$ in $(0,\lambda ^*)$.

Submitted April 22, 1997. Published August 19, 1997.
Math Subject Classification: 35J20, 35J25.
Key Words: Mountain Pass Theorem, Ekeland Variational Principle.

Show me the PDF file (165 KB), TEX file, and other files for this article.

C. O. Alves
Universidade Federal da Paraiba PB, Brasil
e-mail: coalves@dme.ufpb.br
Return to the EJDE home page