Joao Marcos B. do O
Abstract:
Using a variational approach, we investigate the existence of solutions
for non-autonomous perturbations of the
p-Laplacian eigenvalue problem
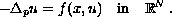
Under the assumptions that the primitive
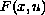 of
of
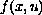 interacts only with the first eigenvalue, we look for solutions in
the space
interacts only with the first eigenvalue, we look for solutions in
the space
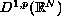 .
Furthermore, we assume a condition that measures how different the
behavior of the function
.
Furthermore, we assume a condition that measures how different the
behavior of the function
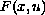 is
from that of the p-power of
is
from that of the p-power of
Submitted January 24, 1997. Published July 15, 1997.
Math Subject Classification: 35A15, 35J60.
Key Words: Mountain Pass Theorem, Palais-Smale Condition,
First eigenvalue,
Show me the PDF file (216 KB), TEX file, and other files for this article.
 |
Joao Marcos B. do O Universidade Federal da Paraiba 58059.900 Joao Pessoa, Pb Brazil e-mail: jmbo@mat.ufpb.br |
|---|
Return to the EJDE web page