Values of
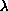 are determined for which there exist solutions in a
cone of the
are determined for which there exist solutions in a
cone of the
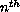 order nonlinear differential equation,
order nonlinear differential equation,
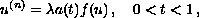
satisfying the multipoint boundary conditions,
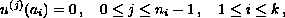
where
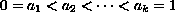 , and
, and
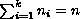 ,
,
where
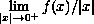 and
and
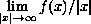 exist.
exist.
Paul W. Eloe & Johnny Henderson
Abstract:
Values of
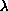 are determined for which there exist solutions in a
cone of the
are determined for which there exist solutions in a
cone of the
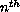 order nonlinear differential equation,
order nonlinear differential equation,
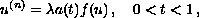
satisfying the multipoint boundary conditions,
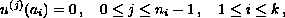
where
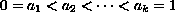 , and
, and
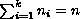 ,
,
where 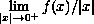 and
and
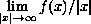 exist.
exist.
Submitted December 17, 1996. Published January 22, 1997.
Math Subject Classification: 34B10, 34B15.
Key Words: multipoint, nonlinear eigenvalue problem, cone.
Show me the PDF file (165 KB), TEX file, and other files for this article.
Johnny Henderson
department of Mathematics,
Auburn University,
Auburn, AL 36849 USA
e-mail: hendej2@mail.auburn.edu