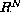Electron. J. Diff. Eqns., Vol. 1996(1996), No. 09, pp. 1-11.

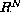ON ELLIPTIC EQUATIONS IN $R^N$ WITH CRITICAL EXPONENTS

C.O. Alves, J.V. Goncalves, & O.H. Miyagaki

Abstract:
In this note we use variational arguments -namely Ekeland's Principle and the Mountain Pass Theorem- to study the equation
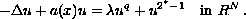
$$-\Delta u + a(x)u = \lambda u^q + u^{2^*-1}\quad {\rm in\ } R^N\,.$$
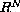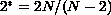The main concern is overcoming compactness difficulties due both to the unboundedness of the domain $R^N$, and the presence of the critical exponent $2^*= 2N/(N-2)$.

Submitted August 7, 1996. Published October 22, 1996.
Math Subject Class.: 35J20, 35K20.
Key Words: Elliptic equations, unbounded domains, critical exponents, variational methods.

Show me the PDF file (176 KB), TEX file, and other files for this article.

C.O. Alves
Dep. Mat. Univ. Fed. Paraiba, 58109-970 - Campina Grande(PB), Brasil
E-mail coalves@dme.ufpb.br

J.V. Goncalves
Dep. Mat. Univ. Brasilia, 70.910-900 Brasilia(DF), Brasil
E-mail jv@mat.unb.br

O.H. Miyagaki
Dep. Mat. Univ. Fed. Vicosa, 36570-000 Vicosa(MG), Brasil
E-mail olimpio@mail.ufv.br

Return to the EJDE home page.