Electron. J. Diff. Eqns., Vol. 1996(1996), No. 07, pp. 1-12.

Radially Symmetric Solutions for a Class of Critical Exponent Elliptic Problems in $R^N$

C. O. Alves, D. C. de Morais Filho, & M. A. S. Souto

Abstract:
We give a method for obtaining radially symmetric solutions for the critical exponent problem
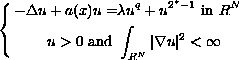
$$\left\{ \eqalign{ -\Delta u+a(x)u=& \lambda u^q+u^{2^*-1}{\rm\ in\ } R^N \cr u{\rm greater thn 0 and\ }&\int_{R^N}|\nabla u|^2 less than \infty\cr } \right. $$
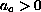where, outside a ball centered at the origin, the non-negative function a is bounded from below by a positive constant $a_o$ greater than 0. We remark that, differently from the literature, we do not require any conditions on a at infinity.

Submitted July 04, 1996. Published: August 30, 1996.
Math Subject Classification: 35A05, 35A15 and 35J20.
Key Words: Radial solutions, critical Sobolev exponents, Palais-Smale condition, Mountain Pass Theorem.

Show me the PDF file (188 KB), TEX file, and other files for this article.

Claudianor O. Alves (coalves@dme.ufpb.br)
Daniel C. de Morais Filho (daniel@dme.ufpb.br)
Marco Aurelio S. Souto} (marco@dme.ufpb.br)
Departamento de Matematica e Estatistica, Centro de Ciencias e Tecnologia, Universidade Federal da Paraiba, Caixa Postal 10044, CEP 58.109-970 - Campina Grande - Paraiba - Brazil
Return to the EJDE home page.