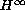Electron. J. Diff. Eqns., Vol. 1995(1995), No. 13, pp 1-17.

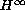Dichotomy and $H^\infty$ Functional Calculi

R. deLaubenfels & Y. Latushkin

Abstract:
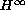Dichotomy for the abstract Cauchy problem with any densely defined closed operator on a Banach space is studied. We give conditions under which an operator with an $H^\infty$ functional calculus has dichotomy. For the operators with imaginary axis contained in the resolvent set and with polynomial growth of the resolvent along the axis we prove the existence of dichotomy on subspaces and superspaces. 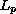Applications to the dichotomy of operators on $L_p$-spaces are given. The principle of linearized instability for nonlinear equations is proved.

Submitted August 1, 1995. Published September 21, 1995.
Math Subject Classification: 47D05, 47A60.
Key Words: Abstract Cauchy problem, operator semigroups, exponential dichotomy, functional calculi.

Show me the PDF file (267 KB), TEX file, and other files for this article.

R. DeLaubenfels
Scientia Research Institute, P.O. Box 988, Athens, OH 45701 USA
e-mail address: 72260.2403@compuserve.com

Y. Latushkin
Department of Mathematics, University of Missouri, Columbia MO 65211 USA
e-mail address: yuri@math.missouri.edu

Return to the EJDE home page.