Solutions that are positive with respect to a cone are obtained for the boundary value problem,
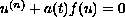 ,
,
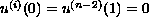 ,
,
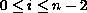 ,
in the cases that
,
in the cases that
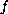 is either superlinear or sublinear. The methods
involve application of a fixed point theorem for operators on a cone.
is either superlinear or sublinear. The methods
involve application of a fixed point theorem for operators on a cone.
Paul W. Eloe & Johnny Henderson
Abstract:
Solutions that are positive with respect to a cone are
obtained for the boundary value problem,
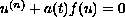 ,
,
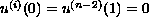 ,
,
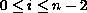 ,
in the cases that
,
in the cases that
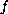 is either superlinear or sublinear. The methods
involve application of a fixed point theorem for operators on a cone.
is either superlinear or sublinear. The methods
involve application of a fixed point theorem for operators on a cone.
Submitted December 4, 1994. Published March 2, 1995.
Math Subject Classification: 34B15.
Key words: Boundary value problems, positive solutions,
superlinear and sublinear, operators on a cone.
Show me the PDF file (141 KB), TEX file, and other files for this article.
Johnny Henderson
Discrete and Statistical Sciences,
Auburn University,
Auburn, AL 36849-5307 USA
e-mail: hendej2@mail.auburn.edu