Electron.n. J. Diff. Eqns. Vol. 1993(1993), No. 02, pp. 1-10.
A singular perturbation problem in integrodifferential equations
James H. Liu
Abstract:
Consider the singular perturbation problem for
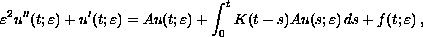
where
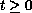 ,
,
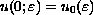 ,
,
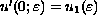 , and
, and
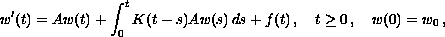
in a Banach space X when
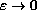 .
Here A is the generator of a strongly continuous cosine family
and a
strongly continuous semigroup, and
.
Here A is the generator of a strongly continuous cosine family
and a
strongly continuous semigroup, and
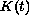 is a bounded linear operator for
is a bounded linear operator for
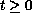 . With some convergence conditions on initial data and
. With some convergence conditions on initial data and
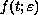 and smoothness conditions on
and smoothness conditions on
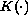 , we prove
that when
, we prove
that when
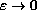 , one has
, one has
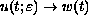 and
and
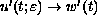 in X uniformly on
[0,T] for any fixed
in X uniformly on
[0,T] for any fixed
 .
An application to viscoelasticity is given.
.
An application to viscoelasticity is given.
Submitted June 14, 1993. Published September 16, 1993.
Math Subject Classification: 45D, 45J, 45N.
Key Words: Singular perturbation, Convergence in solutions and
derivatives.
Show me the
PDF file (139 KB),
TEX file, and other files for this article.
James H. Liu
Department of Mathematics,
James Madison University
Harrisonburg, VA 22807, USA
e-mail: liu@math.jmu.edu
Return to the EJDE home page.
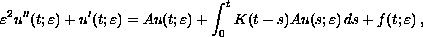
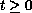 ,
,
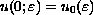 ,
,
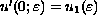 , and
, and
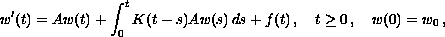
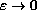 .
Here
.
Here 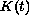 is a bounded linear operator for
is a bounded linear operator for
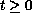 . With some convergence conditions on initial data and
. With some convergence conditions on initial data and
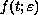 and smoothness conditions on
and smoothness conditions on
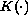 , we prove
that when
, we prove
that when
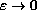 , one has
, one has
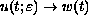 and
and
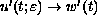 in
in  .
An application to viscoelasticity is given.
.
An application to viscoelasticity is given.