In this monograph we develop an algorithm for constructing Lyapunov functions for arbitrary switched dynamical systems
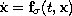 ,
possessing a uniformly asymptotically stable equilibrium.
Let
,
possessing a uniformly asymptotically stable equilibrium.
Let
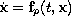 ,
,
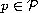 ,
be the collection of the ODEs, to which the switched system corresponds.
The number of the vector fields
,
be the collection of the ODEs, to which the switched system corresponds.
The number of the vector fields
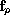 on the right-hand side
of the differential equation is assumed to be finite and we assume that
their components
on the right-hand side
of the differential equation is assumed to be finite and we assume that
their components
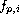 are
are
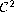 functions and that we
can give some bounds, not necessarily close, on their second-order
partial derivatives.
The inputs of the algorithm are solely a finite number of the
function values of the vector fields
functions and that we
can give some bounds, not necessarily close, on their second-order
partial derivatives.
The inputs of the algorithm are solely a finite number of the
function values of the vector fields
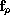 and these bounds.
The domain of the Lyapunov function constructed by the algorithm is
only limited by the size of the equilibrium's region of attraction.
Note, that the concept of a Lyapunov function for the arbitrary switched
system
and these bounds.
The domain of the Lyapunov function constructed by the algorithm is
only limited by the size of the equilibrium's region of attraction.
Note, that the concept of a Lyapunov function for the arbitrary switched
system
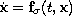 is
equivalent to the concept of a common Lyapunov function for the systems
is
equivalent to the concept of a common Lyapunov function for the systems
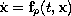 ,
,
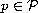 ,
and that if
,
and that if
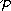 contains exactly one element, then the
switched system is just a usual ODE
contains exactly one element, then the
switched system is just a usual ODE
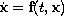 .
We give numerous examples of Lyapunov functions constructed by our
method at the end of this monograph.
.
We give numerous examples of Lyapunov functions constructed by our
method at the end of this monograph.
