Let
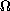 be a domain in
be a domain in
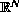 ,
,
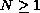 ,
and
,
and
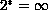 if
if
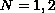 ,
,
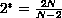 if
if
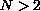 ,
,
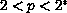 .
. Consider the semilinear elliptic problem
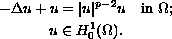
Let
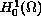 be the Sobolev space in
be the Sobolev space in
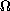 .
The existence, the nonexistence, and the multiplicity of positive
solutions are affected by the geometry and the topology
of the domain
.
The existence, the nonexistence, and the multiplicity of positive
solutions are affected by the geometry and the topology
of the domain
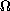 .
The existence, the nonexistence, and the
multiplicity of positive solutions have been the focus of a great
deal of research in recent years.
.
The existence, the nonexistence, and the
multiplicity of positive solutions have been the focus of a great
deal of research in recent years. That the above equation in a bounded domain admits a positive solution is a classical result. Therefore the only interesting domains in which this equation admits a positive solution are proper unbounded domains. Such elliptic problems are difficult because of the lack of compactness in unbounded domains. Remarkable progress in the study of this kind of problem has been made by P. L. Lions. He developed the concentration-compactness principles for solving a large class of minimization problems with constraints in unbounded domains. The characterization of domains in which this equation admits a positive solution is an important open question. In this monograph, we present various analyses and use them to characterize several categories of domains in which this equation admits a positive solution or multiple solutions.
