This paper concerns the equation
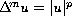 ,
where
,
where
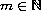 ,
,
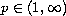 ,
and
,
and
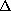 denotes the Laplace operator in
denotes the Laplace operator in
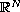 ,
for some
,
for some
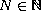 .
Specifically, we are interested in the structure of the set
.
Specifically, we are interested in the structure of the set
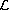 of all large radial solutions
on the open unit ball
of all large radial solutions
on the open unit ball
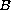 in
in
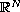 .
In the well-understood second-order case,
the set
.
In the well-understood second-order case,
the set
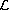 consists of exactly two solutions if
the equation is subcritical, of exactly one solution if it
is critical or supercritical. In the fourth-order case, we show that
consists of exactly two solutions if
the equation is subcritical, of exactly one solution if it
is critical or supercritical. In the fourth-order case, we show that
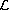 is homeomorphic to the unit circle
is homeomorphic to the unit circle
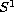 if the equation is subcritical, to
if the equation is subcritical, to
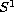 minus a single point if it is critical
or supercritical. For arbitrary
minus a single point if it is critical
or supercritical. For arbitrary
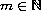 ,
the set
,
the set
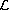 is a full
is a full
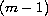 -sphere
whenever the equation is subcritical.
We conjecture, but have not been able to prove in general, that
-sphere
whenever the equation is subcritical.
We conjecture, but have not been able to prove in general, that
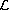 is a punctured
is a punctured
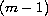 -sphere
whenever the equation
is critical or supercritical. These results and the conjecture
are closely related to the existence and uniqueness (up to scaling)
of entire radial solutions. Understanding the geometric
and topological structure of the set
-sphere
whenever the equation
is critical or supercritical. These results and the conjecture
are closely related to the existence and uniqueness (up to scaling)
of entire radial solutions. Understanding the geometric
and topological structure of the set
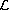 allows precise
statements about the existence and multiplicity of large radial solutions
with prescribed center values
allows precise
statements about the existence and multiplicity of large radial solutions
with prescribed center values
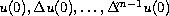 .
.


