In this paper, we obtain some results about the existence of solutions to the system
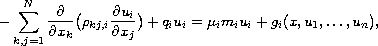
for
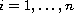 defined in
defined in
 .
.
Laure Cardoulis
Abstract:
In this paper, we obtain some results about the existence of
solutions to the system
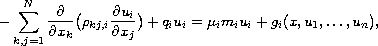
for
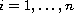 defined in
defined in
 .
.
Published May 15, 2007.
Math Subject Classifications: 35J10.
Key Words: Elliptic systems; sub and super solutions; bifurcation method.
Show me the PDF file (348K), TEX file, and other files for this article.
 |
Laure Cardoulis CeReMath/UMR MIP, University of Toulouse 1 21 allée de Brienne 31000 Toulouse, France email: laure.cardoulis@univ-tlse1.fr |
|---|
Return to the table of contents
for this conference.
Return to the EJDE web page