Electron. J. Differential Equations,
Vol. 2017 (2017), No. 75, pp. 1-22.
Local W^{1,p}-regularity estimates for weak solutions of parabolic
equations with singular divergence-free drifts
Tuoc Phan
Abstract:
We study weighted Sobolev regularity of weak solutions of non-homogeneous
parabolic equations with singular divergence-free drifts. Assuming that the
drifts satisfy some mild regularity conditions, we establish local weighted
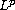 -estimates for the gradients of weak solutions. Our results improve
the classical one to the borderline case by replacing the
-estimates for the gradients of weak solutions. Our results improve
the classical one to the borderline case by replacing the
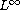 -assumption
on solutions by solutions in the John-Nirenberg BMO space.
The results are also generalized to parabolic equations in divergence form
with small oscillation elliptic symmetric coefficients and therefore improve
many known results.
-assumption
on solutions by solutions in the John-Nirenberg BMO space.
The results are also generalized to parabolic equations in divergence form
with small oscillation elliptic symmetric coefficients and therefore improve
many known results.
Submitted December 31, 2016. Published March 20, 2017.
Math Subject Classifications: 35K10, 35K67, 35B45.
Key Words: Weighted Sobolev estimates; divergence-free drifts;
Muckenhoupt weights; Hardy-Littlewood maximal functions.
Show me the PDF file (338 KB),
TEX file for this article.
 |
Tuoc Phan
Department of Mathematics
University of Tennessee, Knoxville
227 Ayress Hall, 1403 Circle Drive
Knoxville, TN 37996, USA
email: phan@math.utk.edu
|
|---|
Return to the EJDE web page
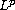 -estimates for the gradients of weak solutions. Our results improve
the classical one to the borderline case by replacing the
-estimates for the gradients of weak solutions. Our results improve
the classical one to the borderline case by replacing the
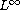 -assumption
on solutions by solutions in the John-Nirenberg BMO space.
The results are also generalized to parabolic equations in divergence form
with small oscillation elliptic symmetric coefficients and therefore improve
many known results.
-assumption
on solutions by solutions in the John-Nirenberg BMO space.
The results are also generalized to parabolic equations in divergence form
with small oscillation elliptic symmetric coefficients and therefore improve
many known results.
