Electron. J. Differential Equations,
Vol. 2017 (2017), No. 61, pp. 1-12.
Classification and evolution of bifurcation curves for the one-dimensional
perturbed Gelfand equation with mixed boundary conditions II
Yu-Hao Liang, Shin-Hwa Wang
Abstract:
In this article, we study the classification and evolution of bifurcation curves
of positive solutions for the one-dimensional perturbed Gelfand equation with
mixed boundary conditions,
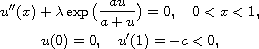
where
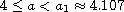 .
We prove that, for
.
We prove that, for
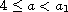 ,
there exist two nonnegative
,
there exist two nonnegative
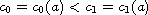 satisfying
satisfying
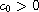 for
for
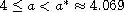 ,
and
,
and
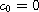 for
for
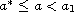 ,
such that, on the
,
such that, on the
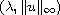 -plane,
(i) when
-plane,
(i) when
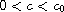 ,
the bifurcation curve is strictly increasing;
(ii) when
,
the bifurcation curve is strictly increasing;
(ii) when
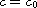 ,
the bifurcation curve is monotone increasing;
(iii) when
,
the bifurcation curve is monotone increasing;
(iii) when
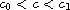 ,
the bifurcation curve is S-shaped;
(iv) when
,
the bifurcation curve is S-shaped;
(iv) when
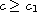 ,
the bifurcation curve is C-shaped. This work
is a continuation of the work by Liang and Wang [8] where
authors studied this problem for
,
the bifurcation curve is C-shaped. This work
is a continuation of the work by Liang and Wang [8] where
authors studied this problem for
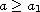 ,
and our results partially
prove a conjecture on this problem for
,
and our results partially
prove a conjecture on this problem for
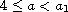 in [8].
in [8].
Submitted November 30, 2016. Published February 28, 2017.
Math Subject Classifications: 34B18, 74G35.
Key Words: Multiplicity; positive solution; perturbed Gelfand equation;
S-shaped bifurcation curve; C-shaped bifurcation curve; time map.
Show me the PDF file (363 KB),
TEX file for this article.
 |
Yu-Hao Liang
Department of Applied Mathematics
National Chiao Tung University
Hsinchu 300, Taiwan
email: yhliang@nctu.edu.tw
|
|---|
 |
Shin-Hwa Wang
Department of Mathematics
National Tsing Hua University
Hsinchu 300, Taiwan
email: shwang@math.nthu.edu.tw
|
|---|
Return to the EJDE web page
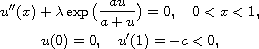
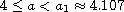 .
We prove that, for
.
We prove that, for
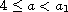 ,
there exist two nonnegative
,
there exist two nonnegative
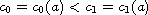 satisfying
satisfying
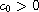 for
for
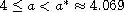 ,
and
,
and
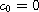 for
for
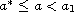 ,
such that, on the
,
such that, on the
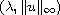 -plane,
(i) when
-plane,
(i) when
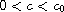 ,
the bifurcation curve is strictly increasing;
(ii) when
,
the bifurcation curve is strictly increasing;
(ii) when
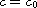 ,
the bifurcation curve is monotone increasing;
(iii) when
,
the bifurcation curve is monotone increasing;
(iii) when
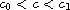 ,
the bifurcation curve is S-shaped;
(iv) when
,
the bifurcation curve is S-shaped;
(iv) when
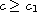 ,
the bifurcation curve is C-shaped. This work
is a continuation of the work by Liang and Wang [8] where
authors studied this problem for
,
the bifurcation curve is C-shaped. This work
is a continuation of the work by Liang and Wang [8] where
authors studied this problem for
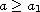 ,
and our results partially
prove a conjecture on this problem for
,
and our results partially
prove a conjecture on this problem for
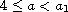 in [8].
in [8].

