Electron. J. Differential Equations,
Vol. 2017 (2017), No. 17, pp. 1-10.
Solvability of boundary-value problems for a linear partial difference equation
Stevo Stevic
Abstract:
In this article we consider the two-dimensional boundary-value problem
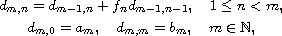
where
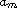 ,
,
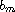 ,
,
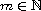 and
and
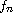 ,
,
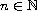 ,
are complex sequences. Employing recently introduced method of half-lines,
it is shown that the boundary-value problem is solvable,
by finding an explicit formula for its solution on the domain,
the, so called, combinatorial domain. The problem is solved
for each complex sequence
,
are complex sequences. Employing recently introduced method of half-lines,
it is shown that the boundary-value problem is solvable,
by finding an explicit formula for its solution on the domain,
the, so called, combinatorial domain. The problem is solved
for each complex sequence
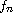 ,
,
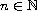 ,
that is, even
if some of its members are equal to zero.
The main result here extends a recent result in the topic.
,
that is, even
if some of its members are equal to zero.
The main result here extends a recent result in the topic.
Submitted October 23, 2016. Published January 14, 2017.
Math Subject Classifications: 39A14, 39A06.
Key Words: Partial difference equation; solvable difference equation;
method of half-lines; combinatorial domain.
Show me the PDF file (223 KB),
TEX file for this article.
 |
Stevo Stevic
Mathematical Institute of the Serbian Academy of Sciences
Knez Mihailova 36/III,
11000 Beograd, Serbia
email: sstevic@ptt.rs
|
|---|
Return to the EJDE web page
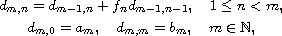
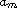 ,
,
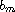 ,
,
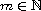 and
and
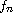 ,
,
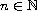 ,
are complex sequences. Employing recently introduced method of half-lines,
it is shown that the boundary-value problem is solvable,
by finding an explicit formula for its solution on the domain,
the, so called, combinatorial domain. The problem is solved
for each complex sequence
,
are complex sequences. Employing recently introduced method of half-lines,
it is shown that the boundary-value problem is solvable,
by finding an explicit formula for its solution on the domain,
the, so called, combinatorial domain. The problem is solved
for each complex sequence
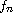 ,
,
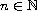 ,
that is, even
if some of its members are equal to zero.
The main result here extends a recent result in the topic.
,
that is, even
if some of its members are equal to zero.
The main result here extends a recent result in the topic.
