Electron. J. Differential Equations,
Vol. 2017 (2017), No. 15, pp. 1-7.
Existence of solutions to asymptotically periodic Schrodinger equations
Marcelo F. Furtado, Reinaldo de Marchi
Abstract:
We show the existence of a nonzero solution for the semilinear
Schrodinger equation
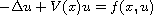 .
The potential V is periodic and 0 belongs to a gap of
.
The potential V is periodic and 0 belongs to a gap of
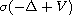 .
The function f is superlinear and asymptotically periodic with respect to
x variable. In the proof we apply a new critical point theorem for
strongly indefinite functionals proved in [3].
.
The function f is superlinear and asymptotically periodic with respect to
x variable. In the proof we apply a new critical point theorem for
strongly indefinite functionals proved in [3].
Submitted July 8, 2016. Published January 13, 2017.
Math Subject Classifications: 35J50, 35J45.
Key Words: Strongly indefinite functionals; Schrodinger equation;
asymptotically periodic problem.
Show me the PDF file (204 KB),
TEX file for this article.
 |
Marcelo F. Furtado
Universidade de Brasília
Departamento de Matemática
70910-900 Brasília-DF, Brazil
email: mfurtado@unb.br
|
|---|
 |
Reinaldo de Marchi
Universidade Federal do Mato Grosso
Departamento de Matemática
78060-900 Cuiabá-MT, Brazil
email: reinaldodemarchi@ufmt.br
|
|---|
Return to the EJDE web page
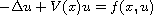 .
The potential V is periodic and 0 belongs to a gap of
.
The potential V is periodic and 0 belongs to a gap of
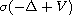 .
The function f is superlinear and asymptotically periodic with respect to
x variable. In the proof we apply a new critical point theorem for
strongly indefinite functionals proved in [3].
.
The function f is superlinear and asymptotically periodic with respect to
x variable. In the proof we apply a new critical point theorem for
strongly indefinite functionals proved in [3].

