Under simple conditions on f and g, we show that existence of positive radial solutions for the quasilinear elliptic equation
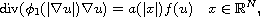
and for the system
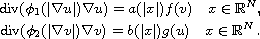
Zhijun Zhang
Abstract:
Under simple conditions on f and g, we
show that existence of positive radial solutions
for the quasilinear elliptic equation
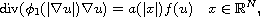
and for the system
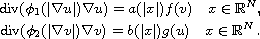
Submitted November 23, 2015. Published February 17, 2016.
Math Subject Classifications: 35J55, 35J60, 35J65.
Key Words: Quasilinear elliptic equation; radial solutions; existence.
Show me the PDF file (221 KB), TEX file for this article.
 |
Zhijun Zhang School of Mathematics and Information Science Yantai University Yantai 264005, Shandong, China email: chinazjzhang2002@163.com, zhangzj@ytu.edu.cn |
|---|
Return to the EJDE web page