Electron. J. Differential Equations,
Vol. 2016 (2016), No. 261, pp. 1-17.
Solutions to semilinear elliptic PDE's with biharmonic operator
and singular potential
Mousomi Bhakta
Abstract:
We study the existence and nonexistence of positive solution to the problem

where
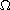 is a smooth bounded domain in
is a smooth bounded domain in
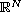 .
We show the existence of a value
.
We show the existence of a value
 such that when
such that when
 , there is a solution
and when
, there is a solution
and when
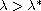 there is no solution
in
there is no solution
in
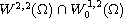 .
Moreover as
.
Moreover as
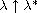 ,
the minimal positive solution
converges to a solution.
We also prove that there exists
,
the minimal positive solution
converges to a solution.
We also prove that there exists
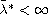 with
with
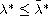 ,
and for
,
and for
 ,
such that the above problem does not have solution even in the distributional
sense/very weak sense, and there is a complete blow-up.
Under an additional integrability condition on b, we establish the
uniqueness of positive solution.
,
such that the above problem does not have solution even in the distributional
sense/very weak sense, and there is a complete blow-up.
Under an additional integrability condition on b, we establish the
uniqueness of positive solution.
Submitted February 5, 2016. Published September 28, 2016.
Math Subject Classifications: 35B09, 35B25, 35B35, 35G30, 35J91.
Key Words: Semilinear biharmonic equation; singular potential;
Navier boundary condition; existence; nonexistence;
blow-up phenomenon; stability; uniqueness of extremal solution.
Show me the PDF file (312 KB),
TEX file for this article.
 |
Mousomi Bhakta
Department of Mathematics
Indian Institute of Science Education and Research
Dr. Homi Bhaba road
Pune-411008, India
email: mousomi@iiserpune.ac.in
|
|---|
Return to the EJDE web page

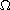 is a smooth bounded domain in
is a smooth bounded domain in
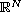 .
We show the existence of a value
.
We show the existence of a value
 such that when
such that when
 , there is a solution
and when
, there is a solution
and when
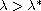 there is no solution
in
there is no solution
in
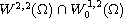 .
Moreover as
.
Moreover as
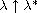 ,
the minimal positive solution
converges to a solution.
We also prove that there exists
,
the minimal positive solution
converges to a solution.
We also prove that there exists
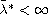 with
with
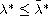 ,
and for
,
and for
 ,
such that the above problem does not have solution even in the distributional
sense/very weak sense, and there is a complete blow-up.
Under an additional integrability condition on b, we establish the
uniqueness of positive solution.
,
such that the above problem does not have solution even in the distributional
sense/very weak sense, and there is a complete blow-up.
Under an additional integrability condition on b, we establish the
uniqueness of positive solution.
