Khadijah Sharaf
Abstract:
We consider an elliptic PDE with critical nonlinearity involving the
Laplacian operator with zero Dirichlet boundary condition on the
unit ball of
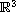 .
We assume some perturbation conditions and obtain what seems to be
the first existence result for this problem.
.
We assume some perturbation conditions and obtain what seems to be
the first existence result for this problem.
Submitted March 8, 2016. Published August 23, 2016.
Math Subject Classifications: 35J65.
Key Words: Critical Sobolev exponent; critical points at infinity;
variational method.
Show me the PDF file (225 KB), TEX file for this article.
| Khadijah Sharaf Department of mathematics King Abdulaziz University, P.O. 80230 Jeddah, Kingdom of Saudi Arabia email: kh_sharaf@yahoo.com |
Return to the EJDE web page