Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 01, pp. 1-15.
Singular regularization of operator equations in L1 spaces via
fractional differential equations
George L. Karakostas, Ioannis K. Purnaras
Abstract:
An abstract causal operator equation y=Ay defined on a space of the
form
![$L_1([0,\tau],X)$](gifs/aa.gif) , with X a Banach space, is regularized
by the fractional differential equation
, with X a Banach space, is regularized
by the fractional differential equation
![$$
\varepsilon(D_0^{\alpha}y_{\varepsilon})(t)
=-y_{\varepsilon}(t)+(Ay_{\varepsilon})(t), \quad t\in[0,\tau],
$$](gifs/ab.gif)
where
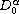 denotes the (left) Riemann-Liouville derivative
of order
denotes the (left) Riemann-Liouville derivative
of order
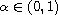 . The main procedure lies on properties of
the Mittag-Leffler function combined with some facts from convolution theory.
Our results complete relative ones that have appeared in the literature;
see, e.g. [5] in which regularization via ordinary differential
equations is used.
. The main procedure lies on properties of
the Mittag-Leffler function combined with some facts from convolution theory.
Our results complete relative ones that have appeared in the literature;
see, e.g. [5] in which regularization via ordinary differential
equations is used.
Submitted June 8, 2015. Published January 4, 2016.
Math Subject Classifications: 34K35, 34A08, 47045, 65J20.
Key Words: Causal operator equations; fractional differential equations;
regularization; Banach space.
Show me the PDF file (252 KB),
TEX file for this article.
 |
George L. Karakostas
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: gkarako@uoi.gr
|
|---|
 |
Ioannis K. Purnaras
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: ipurnara@uoi.gr
|
|---|
Return to the EJDE web page
![$L_1([0,\tau],X)$](gifs/aa.gif) , with X a Banach space, is regularized
by the fractional differential equation
, with X a Banach space, is regularized
by the fractional differential equation
![$$
\varepsilon(D_0^{\alpha}y_{\varepsilon})(t)
=-y_{\varepsilon}(t)+(Ay_{\varepsilon})(t), \quad t\in[0,\tau],
$$](gifs/ab.gif)
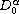 denotes the (left) Riemann-Liouville derivative
of order
denotes the (left) Riemann-Liouville derivative
of order
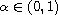 . The main procedure lies on properties of
the Mittag-Leffler function combined with some facts from convolution theory.
Our results complete relative ones that have appeared in the literature;
see, e.g. [5] in which regularization via ordinary differential
equations is used.
. The main procedure lies on properties of
the Mittag-Leffler function combined with some facts from convolution theory.
Our results complete relative ones that have appeared in the literature;
see, e.g. [5] in which regularization via ordinary differential
equations is used.

