Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 86, pp. 1-15.
Existence and multiplicity of solutions for a prescribed
mean-curvature problem with critical growth
Giovany M. Figueiredo, Marcos T. O. Pimenta
Abstract:
In this work we study an existence and multiplicity of solutions for the
prescribed mean-curvature problem with critical growth,
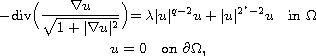
where
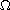 is a bounded smooth domain of
is a bounded smooth domain of
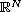 ,
,
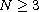 and
and
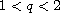 .
To employ variational arguments, we consider
an auxiliary problem which is proved to have infinitely many solutions
by genus theory. A clever estimate in the gradient of the solutions of the
modified problem is necessary to recover solutions of the original problem.
.
To employ variational arguments, we consider
an auxiliary problem which is proved to have infinitely many solutions
by genus theory. A clever estimate in the gradient of the solutions of the
modified problem is necessary to recover solutions of the original problem.
Submitted March 24, 2014. Published April 7, 2015.
Math Subject Classifications: 35J93, 35J62, 35J20.
Key Words: Prescribed mean-curvature problem; critical exponent;
variational methods.
Show me the PDF file (280 KB),
TEX file, and other files for this article.
 |
Giovany M. Figueiredo
Universidade Federal do Pará
Faculdade de Matemática
CEP: 66075-110 Belém - Pa, Brazil
email: giovany@ufpa.br
|
|---|
 |
Marcos T. O. Pimenta
Faculdade de Ciências e Tecnlogia
UNESP - Univ Estadual Paulista
19060-900, Presidente Prudente - SP, Brazil
Phone (55) 18 - 3229-5625 FAX (55) 18 - 3221-8333
email: pimenta@fct.unesp.br
|
|---|
Return to the EJDE web page
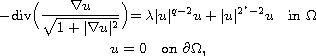
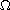 is a bounded smooth domain of
is a bounded smooth domain of
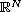 ,
,
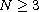 and
and
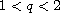 .
To employ variational arguments, we consider
an auxiliary problem which is proved to have infinitely many solutions
by genus theory. A clever estimate in the gradient of the solutions of the
modified problem is necessary to recover solutions of the original problem.
.
To employ variational arguments, we consider
an auxiliary problem which is proved to have infinitely many solutions
by genus theory. A clever estimate in the gradient of the solutions of the
modified problem is necessary to recover solutions of the original problem.

