Electron. J. Diff. Equ., Vol. 2015 (2015), No. 170, pp. 1-24.

Local and global low-regularity solutions to generalized Leray-alpha equations

Nathan Pennington

Abstract:
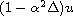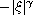It has recently become common to study approximating equations for the Navier-Stokes equation. One of these is the Leray-alpha equation, which regularizes the Navier-Stokes equation by replacing (in most locations) the solution u with $(1-\alpha^2\Delta)u$. 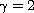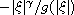Another is the generalized Navier-Stokes equation, which replaces the Laplacian with a Fourier multiplier with symbol of the form $-|\xi|^\gamma$ ( $\gamma=2$ is the standard Navier-Stokes equation), and recently in [16] Tao also considered multipliers of the form $-|\xi|^\gamma/g(|\xi|)$, where g is (essentially) a logarithm. The generalized Leray-alpha equation combines these two modifications by incorporating the regularizing term and replacing the Laplacians with more general Fourier multipliers, including allowing for g terms similar to those used in [16]. Our goal in this paper is to obtain existence and uniqueness results with low regularity and/or non-L^2 initial data. We will also use energy estimates to extend some of these local existence results to global existence results.

Submitted May 15, 2015. Published June 18, 2015.
Math Subject Classifications: 76D05, 35A02, 35K58.
Key Words: Leray-alpha model; Besov space; fractional Laplacian.

Show me the PDF file (332 KB), TEX file, and other files for this article.

Nathan Pennington
Department of Mathematics, Creighton University
2500 California Plaza
Omaha, NE 68178, USA
email: nathanpennington@creighton.edu

Return to the EJDE web page