In this article, we study the bifurcation of limit cycles from the harmonic oscillator
,
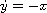in the system
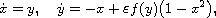
where
is a small positive parameter tending
to 0 and f is an odd polynomial of degree 2n + 1, with n an arbitrary
but fixed natural number. We prove that, the above differential system,
in the global plane, for particularly chosen odd polynomials f of degree
2n + 1 has exactly n + 1 limit cycles and that this number is an
upper bound for the number of limit cycles for every case of an arbitrary
odd polynomial f of degree 2n + 1. More specifically, the existence of
the limit cycles, which is the first of the main results in this work,
is obtained by using the Poincare's method, and the upper bound for the
number of limit cycles can be derived from the work of Iliev [4].
We also investigate the possible relative positions of the limit cycles
for this differential system, which is the second main problem studying
in this work. In particular, we construct differential systems with n given
limit cycles and one limit cycle whose position depends on the position of
the previous n limit cycles. Finally, we give some examples in order to
illustrate the general theory presented in this work.
