Using the power series method, we solve the inhomogeneous linear first order differential equation
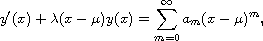
and prove an approximation property of Gaussian functions.
Soon-Mo Jung, Hamdullah Sevli, Sebaheddin Sevgin
Abstract:
Using the power series method, we solve the inhomogeneous
linear first order differential equation
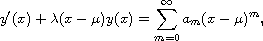
and prove an approximation property of Gaussian functions.
Submitted October 5, 2012. Published January 7, 2013.
Math Subject Classifications: 34A30, 34A40, 41A30, 39B82, 34A25.
Key Words: Linear first order differential equation;
power series method; Gaussian function; approximation;
Hyers-Ulam stability; local Hyers-Ulam stability.
Show me the PDF file (201 KB), TEX file, and other files for this article.
 |
Soon-Mo Jung Mathematics Section, College of Science and Technology Hongik University, 339-701 Jochiwon, South Korea email: smjung@hongik.ac.kr |
|---|---|
 |
Hamdullah Sevli Department of Mathematics, Faculty of Sciences and Arts Istanbul Commerce University 34672 Uskudar, Istanbul, Turkey email: hsevli@yahoo.com |
 |
Sebaheddin Sevgin Department of Mathematics, Faculty of Art and Science Yuzuncu Yil University, 65080 Van, Turkey email: ssevgin@yahoo.com |
Return to the EJDE web page