Under the assumption that the potential W is invariant under a general discrete reflection group
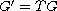acting
on
,
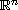we establish existence of G'-equivariant
solutions to
,
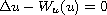and find an estimate.
By taking the size of the cell of the lattice in space domain
to infinity, we obtain that these solutions converge to
G-equivariant solutions connecting the minima of the potential
W along certain directions at infinity. When particularized to
the nonlinear harmonic oscillator
,
,
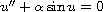the solutions correspond to those in the phase plane
above and below the heteroclinic connections,
while the G-equivariant solutions captured in the limit
correspond to the heteroclinic connections themselves.
Our main tool is the G'-positivity of the parabolic semigroup
associated with the elliptic system which requires only
the hypothesis of symmetry for W. The constructed solutions
are positive in the sense that as maps from
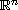into
itself leave the closure of the fundamental alcove (region) invariant.
