Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 98, pp. 1-13.
Existence and multiplicity of solutions for a singular
semilinear elliptic problem in R^2
Manasses de Souza
Abstract:
Using minimax methods we study the existence and multiplicity of
nontrivial solutions for a singular class of semilinear elliptic
nonhomogeneous equation where the potentials can change sign and
the nonlinearities may be unbounded in
 and behaves like
and behaves like
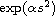 when
when
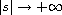 .
We establish the
existence of two distinct solutions when the perturbation is
suitable small.
.
We establish the
existence of two distinct solutions when the perturbation is
suitable small.
Submitted May 2, 2011. Published August 3, 2011.
Math Subject Classifications: 35J60, 35J20, 35B33.
Key Words: Variational methods; Trudinger-Moser inequality;
critical points; critical exponents.
Show me the PDF file (265 KB),
TEX file, and other files for this article.
 |
Manasses de Souza
Departamento de Matemática
Universidade Federal da Paraíba
58.051-900 João Pessoa, PB, Brazil
email: manasses@mat.ufpb.br
|
|---|
Return to the EJDE web page
 and behaves like
and behaves like
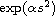 when
when
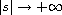 .
We establish the
existence of two distinct solutions when the perturbation is
suitable small.
.
We establish the
existence of two distinct solutions when the perturbation is
suitable small.
