Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 67, pp. 1-15.
Vanishing p-capacity of singular sets for p-harmonic functions
Tomohiko Sato, Takashi Suzuki, Futoshi Takahashi
Abstract:
In this article, we study a counterpart of the removable
singularity property of
 -harmonic functions.
It is shown that p-capacity of the singular set of any
-harmonic functions.
It is shown that p-capacity of the singular set of any
 -harmonic
function vanishes, and such function is always
weakly
-harmonic
function vanishes, and such function is always
weakly
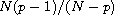 -integrable. Several related results
are also shown.
-integrable. Several related results
are also shown.
Submitted April 4, 2011. Published May 18, 2011.
Math Subject Classifications: 35B05, 35B45, 35J15, 35J70.
Key Words: p-harmonic function; capacity; singular set;
removable singularity; weak Sobolev space.
Show me the PDF file (265 KB),
TEX file, and other files for this article.
 |
Tomohiko Sato
Department of Mathematics, Faculty of Science
Gakushuin University
1-5-1 Mejiro, Toshima-ku, Tokyo, 171-8588, Japan
email: tomohiko.sato@gakushuin.ac.jp
|
|---|
 |
Takashi Suzuki
Division of Mathematical Science,
Department of System Innovation
Graduate School of Engineering Science, Osaka University
Machikaneyamacho 1-3, Toyonakashi, 560-8531, Japan
email: suzuki@sigmath.es.osaka-u.ac.jp
|
|---|
 |
Futoshi Takahashi
Department of Mathematics, Graduate School of Science
Osaka City University
Sugimoto 3-3-138, Sumiyoshiku, Osakashi, 535-8585, Japan
email: futoshi@sci.osaka-cu.ac.jp
|
|---|
Return to the EJDE web page
 -harmonic functions.
It is shown that p-capacity of the singular set of any
-harmonic functions.
It is shown that p-capacity of the singular set of any
 -harmonic
function vanishes, and such function is always
weakly
-harmonic
function vanishes, and such function is always
weakly
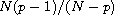 -integrable. Several related results
are also shown.
-integrable. Several related results
are also shown.


