We derive rigorously a homogenized model for the displacement of one compressible miscible fluid by another in a partially fractured porous reservoir. We denote by
the characteristic size of
the heterogeneity in the medium. A function
characterizes
the cracking degree of the rock.
Our starting point is an adapted microscopic model which is scaled by
appropriate powers of
.
We then study its limit as
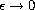. Because of the partially fractured character of
the medium, the equation expressing the conservation of total mass
in the flow is of degenerate parabolic type.
The homogenization process for this equation is thus nonstandard.
To overcome this difficulty, we adapt two-scale convergence techniques,
convexity arguments and classical compactness tools. The homogenized
model contains both single porosity and double porosity characteristics.
