Let
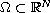 , with
, with
 ,
be a Lipschitz
domain and let
,
be a Lipschitz
domain and let
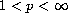 .
We consider the eigenvalue problem
.
We consider the eigenvalue problem
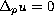 in
in
 and
and
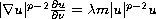 on
on
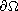 ,
where
,
where
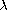 is the eigenvalue and
is the eigenvalue and
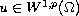 is an associated eigenfunction.
The weight
is an associated eigenfunction.
The weight
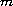 is assumed to lie in an appropriate Lebesgue space
and may change sign. We sketch how a sequence of eigenvalues may
be obtained using infinite dimensional Ljusternik-Schnirelman
theory and we investigate some of the nodal properties of
eigenfunctions associated to the first and second eigenvalues.
Amongst other results we find that if
is assumed to lie in an appropriate Lebesgue space
and may change sign. We sketch how a sequence of eigenvalues may
be obtained using infinite dimensional Ljusternik-Schnirelman
theory and we investigate some of the nodal properties of
eigenfunctions associated to the first and second eigenvalues.
Amongst other results we find that if
 and
and
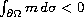 then the first positive
eigenvalue is the only eigenvalue associated to an eigenfunction
of definite sign and any eigenfunction associated to the second
positive eigenvalue has exactly two nodal domains.
then the first positive
eigenvalue is the only eigenvalue associated to an eigenfunction
of definite sign and any eigenfunction associated to the second
positive eigenvalue has exactly two nodal domains.
