We consider a boundary-value problem of the form
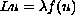 ,
where
,
where
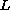 is a
is a
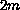 -th
order disconjugate ordinary differential operator
(
-th
order disconjugate ordinary differential operator
(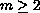 is an integer),
is an integer),
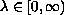 ,
and the function
,
and the function
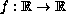 is
is
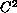 and
satisfies
and
satisfies
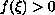 ,
,
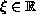 .
Under various convexity or concavity type assumptions on
.
Under various convexity or concavity type assumptions on
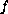 we show that this problem has a smooth curve,
we show that this problem has a smooth curve,
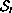 ,
of solutions
,
of solutions
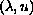 ,
emanating from
,
emanating from
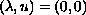 ,
and we describe the shape and asymptotes of
,
and we describe the shape and asymptotes of
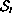 .
All the solutions on
.
All the solutions on
 are positive
and all solutions for which
are positive
and all solutions for which
 is stable lie on
is stable lie on
 .
.
