Electron. J. Diff. Eqns., Vol. 2004(2004), No. 146, pp. 1-14.
Resolvent estimates for scalar fields with electromagnetic perturbation
Mirko Tarulli
Abstract:
In this note we prove some estimates for the resolvent of the
operator
 perturbed by the differential operator
perturbed by the differential operator
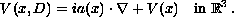
This differential operator is of short range type
and a compact perturbation of the Laplacian on
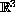 .
Also we find estimates in the space-time norm for the solution
of the wave equation with such perturbation.
.
Also we find estimates in the space-time norm for the solution
of the wave equation with such perturbation.
Submitted July 12, 2004. Published December 7, 2004.
Math Subject Classifications: 35L05, 35J10, 35P25, 35B25, 35B34, 35B40.
Key Words: Perturbed wave equation; perturbed Schrodinger equation;
perturbed Dirac equation; resolvent; short range perturbation;
smoothing estimates.
Show me the
PDF file (289K),
TEX file, and other files for this article.
 |
Mirko Tarulli
Dipartimento di Matematica
Universitá di Pisa
Via F. Buonarroti 2, 56127 Pisa, Italy
email: tarulli@mail.dm.unipi.it |
|---|
Return to the EJDE web page
 perturbed by the differential operator
perturbed by the differential operator
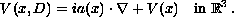
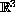 .
Also we find estimates in the space-time norm for the solution
of the wave equation with such perturbation.
.
Also we find estimates in the space-time norm for the solution
of the wave equation with such perturbation.
