Electron. J. Diff. Eqns., Vol. 2003(2003), No. 89, pp. 1-12.
Positive solutions of boundary-value problems for
2m-order differential equations
Yuji Liu & Weigao Ge
Abstract:
This article concerns the existence of positive
solutions to the differential equation
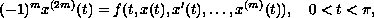
subject to boundary condition
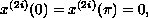
or to the boundary condition
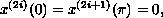
for
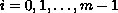 .
Sufficient conditions for the
existence of at least one positive solution of each
boundary-value problem are established.
Motivated by references [7,17,21], the emphasis in
this paper is that
.
Sufficient conditions for the
existence of at least one positive solution of each
boundary-value problem are established.
Motivated by references [7,17,21], the emphasis in
this paper is that
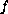 depends on all higher-order derivatives.
depends on all higher-order derivatives.
Submitted June 23, 2003. Published September 4, 2003.
Math Subject Classifications: 34B18, 34B15, 34B27
Key Words: Higher-order differential equation, boundary-value problem,
positive solution, fixed point theorem
Show me the
PDF file (210K),
TEX file, and other files for this article.
 |
Yuji Liu
Department of Mathematics
Beijing Institute of Technology
Beijing, 100081, China
Department of Applied Mathematics
Hunan Institute of Technology,
Hunan, 414000, China
email: liuyuji888@sohu.com
|
|---|
| |
Weigao Ge
Department of Applied Mathematics
Beijing Institute of Technology
Beijing, 100081, China |
|---|
Return to the EJDE web page
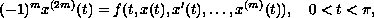
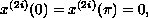
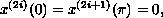
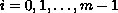 .
Sufficient conditions for the
existence of at least one positive solution of each
boundary-value problem are established.
Motivated by references [7,17,21], the emphasis in
this paper is that
.
Sufficient conditions for the
existence of at least one positive solution of each
boundary-value problem are established.
Motivated by references [7,17,21], the emphasis in
this paper is that
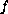 depends on all higher-order derivatives.
depends on all higher-order derivatives.
